Juros Compostos e o Número de Euler (e)

Pedro Lula Mota é editor do Terraço Econômico

O número de Euler, mais conhecido pela letra e, é um daqueles números especiais. Para quem é admirador da beleza da matemática e de seus fenômenos, o número carrega grande significado, sendo uma das mais importantes constantes reais.

Interessante que seu parente mais próximo e famoso, o Pi (Π), já tinha suas propriedades conhecidas em tempos antigos, sendo citado nas passagens bíblicas e trabalhos de Arquimedes (287 a 212 a.C.). Contudo, o número de Euler só foi de fato comprovado muito, mas muito tempo depois [1].

Segundo registros [2], acredita-se que sua primeira “aparição” se deu em situações práticas no cálculo de juros compostos, no início do século XVII, período em que a efervescência do capitalismo crescia e o volume das transações financeiras aumentava. Na explosão da ganância, mercadores e banqueiros emprestavam e investiam à taxa de juros de mercado, com objetivo de acumular mais riquezas e, indiretamente, oferecer liquidez ao sistema.

Vamos olhar a questão desde o início. Por exemplo, em uma transação corriqueira, em que se empresta a quantia de $ 100 a serem pagos ao fim de um ano, considerando que a remuneração deste capital ocorreria à taxa de 10% a.a. (sempre lembrando que juros é o preço do dinheiro no tempo), o valor devido ao fim de um ano será de $110. Caso o devedor não tivesse o valor para pagar na data acordada, o banqueiro poderia lhe conceder uma renovação, capitalizando os 10%a.a. de juros sobre o novo valor de R$110. Ao fim de mais um ano, o valor devido seria de $ 121 – no caso do devedor ainda continuar ilíquido, a renovação ocorre mais uma vez e o ciclo reinicia. Interessante notar que o montante cresce em uma progressão geométrica de razão 1,10.

Eis que um belo dia, o banqueiro, muito sabiamente, decidiu aplicar a mesma taxa de juros, mas em período de capitalização menor, ou seja, a contabilização de juros para o montante passou a ser em período menor que um ano. Podendo ser semestral, trimestral, mensal, diário, por segundo, ou a cada período n, podendo n ser tão pequeno, que tem-se continuamente o acréscimo de juros e, assim, um belo axioma matemático surge. Transformando a situação do empréstimo em uma formula matemática, teremos o  para o montante inicial emprestado, a taxa de juros (r), (n) a quantidade de capitalizações dentro do período informado e (t) o tempo total da operação, no caso 1 ano. Definimos:

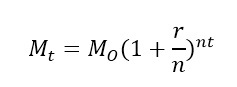
Sendo assim, para o valor empresado orginalmente pelo banqueiro ($ 100) teremos os seguintes resultados, em função do tipo de capitalização aplicada.

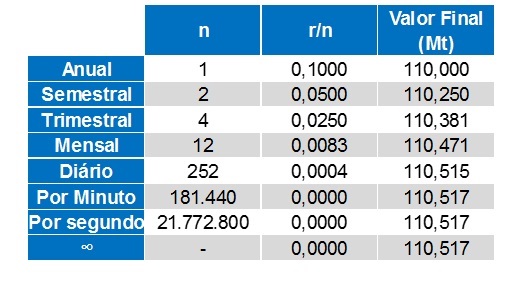
Nota-se que à medida que a frequência dos períodos aumenta, o montante final a ser pago é cada vez maior (mesmo que em escala decimal), e, ainda, que a cada aumento na frequência, a diferença entre o valor calculado e seu antecessor se torna menor. A diferença entre o resultado anual e semestral é visível, porém em casos extremos de minutos e segundos, ela é insignificante, ou seja, existe um limite implícito que deriva da própria matemática.

Outro conceito importante de finanças também é evidenciado, no qual a taxa de juros NOMINAL informada é de 10%a.a., porém a taxa EFETIVA na operação se revela maior, o que reflete no maior montante de juros pagos ao banqueiro. Podemos então extrapolar essas taxas para t = 16 anos e analisar o comportamento acumulado. Novamente, a diferença entre elas tende a diminuir a à medida que o número de capitalizações tende a números enormes.

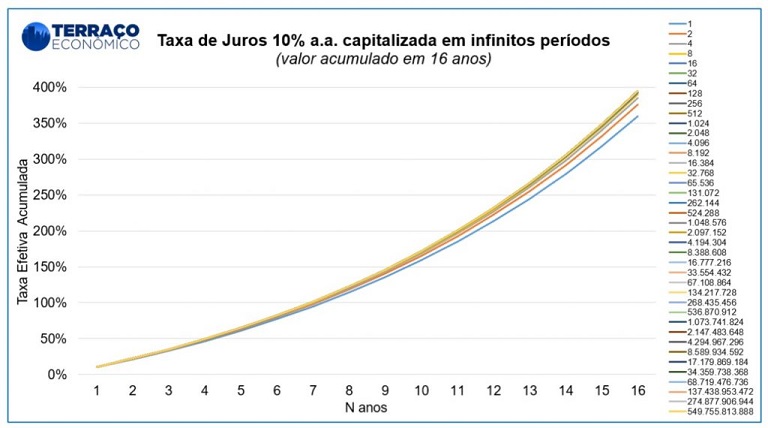
Mas então para que servem todas essas derivações matemáticas? Para demonstrar como operavam os banqueiros na época (também atualmente) e como conseguiam extrair o máximo de juros dos empréstimos cobrados. Contudo, mais importante que isso é entender que por uma questão estritamente aritmética, a simples mudança no período de capitalização não consegue aumentar a cobrança de juros infinitamente, pois existe um limite de crescimento natural nesse processo.

Observando aquela nossa primeira equação apresentada, Os matemáticos se perguntaram o que aconteceria se a taxa de juros fosse aplicada continuamente – ou seja, sobre frações cada vez menores do período.  O padrão agora, de contabilização de juros, fica em n partes iguais, como uma taxa de juros 1/n :

 

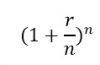
Juros compostos continuamente correspondem a usar um n extremante grande. Fazendo isso e mais uns cálculos, encontramos Algo como na tabela abaixo (vamos usar dez casas decimais nas contas):

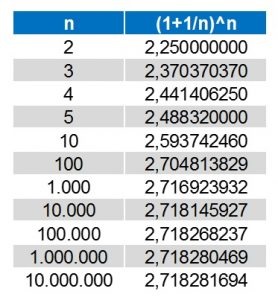
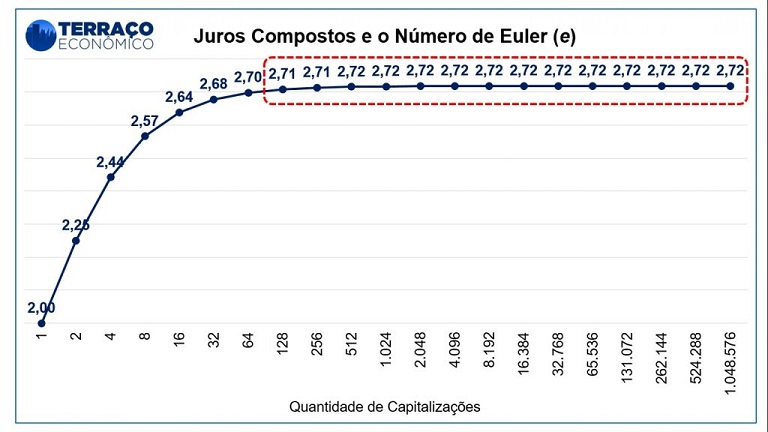
Et voilà, eis que surge paulatinamente um padrão, mesmo ao aumentar o valor n. Precisaríamos adotar valores muito grandes de n para ver efetivamente o padrão, mas notamos que, no limite, à medida que o n aumenta, o fator multiplicador de juros se aproxima de um número fixo, aproximadamente igual a 2,71828. Isto de fato é verdade, e observando o gráfico abaixo, fica mais fácil de notar que: ao aumentar o valor de n (número de capitalizações) o valor do multiplicador de juros atinge um valor e estaciona nele, indefinidamente.

Os matemáticos chamam esse número especial de e, sendo que, matematicamente:

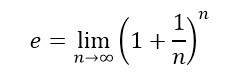
O símbolo “lim” significa que “n se torne infinitamente grande”. E por e se tratar de um número irracional, o apresentamos sua forma com 100 casas, para efeito de curiosidade:

e=2,71828182845904523536028747135266249775724709369995957496696762772407663035354759451382178525166427…

Esse é outro daqueles números curiosos que, como o Pi, tem uma expansão decimal que continua ad infinitum, mas que jamais repete o mesmo bloco de dígitos. A prova disto foi confirmada pelo matemático suíço Euler em 1737, na sua obra chamada Introcutio in analysin infinitorum, extenso trabalho que procurava analisar os vários comportamentos sobre séries infinitas e frações contínuas, sendo o primeiro a chamar a atenção para o singelo número que de forma recorrente aparecia em suas funções. Como era conhecido por sua formalidade na matemática, Euler pode constatar a característica de irracionalidade do número de forma precisa e nunca antes confirmada.

Para completar o raciocínio, aplicando o conceito de capitalização contínua, e entendendo como isso leva ao famoso número de Euler (e), podemos ver como ficaria a situação do empréstimo com o banqueiro, porém agora contabilizando juros na maior frequência possível:

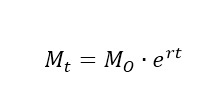
Vale ressaltar, para os mais atentos, que o número também é conhecido como número de Napier, número neperiano ou número exponencial. Como citamos, sua propriedade já era antiga conhecida, especialmente nos estudos do escocês Jonh Napier sobre logaritmos (do grego logos de “proporção”, e arithmos, “números”) oferecendo o pontapé essencial para o cálculo de números complicados multiplicados por raízes quadradas ou cúbicas. Considerando tempos de baixa tecnologia, somar dois números decimais podia ser fácil, mas multiplica-los era bem mais difícil. Assim, Neper inventou um método de transformar multiplicação em adição. A mágica foi trabalhar com potencias de um número fixo e assim nasceram então os logaritmos.

As aplicações do número de Euler são inúmeras e derivam de uma série de outros fenômenos importantes, que são encontrados não só nas finanças, mas economia, física, engenharia, biologia, astronomia e etc, e que validam a teoria de que há certa harmonia entra a matemática e a natureza.

Por fim, vale citar que o matemático Euler, do alto da sua genialidade, desenvolveu o que é conhecido como a formula mais bela de toda a matemática, unindo duas grandes constantes do mundo da matemática:

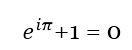
A formula pode ser explicada usando uma conexão surpreendente entre as funções exponencial complexa e trigonométrica e que deu origem à teoria dos números complexos, muito usada na engenharia elétrica, por exemplo. Mas aí é assunto para outro artigo.

Pedro Lula Mota, editor do Terraço Econômico

Rubens Terra,  Engenheiro mecânico formado pela POLI-USP e candidato ao Level II do CFA Program. Atuou durante anos no mercado financeiro,  no mercado de educação e como empreendedor.  É sócio-fundador da Beat The Market Co

[1] E. Maor: e: A história de um número. Editora Record, 2008

[2] C. B. Boyer: História da Matemática. Edgard Blücher, 2a ed., 1996